brelans: conservation de l’énergie et de l’impulsion

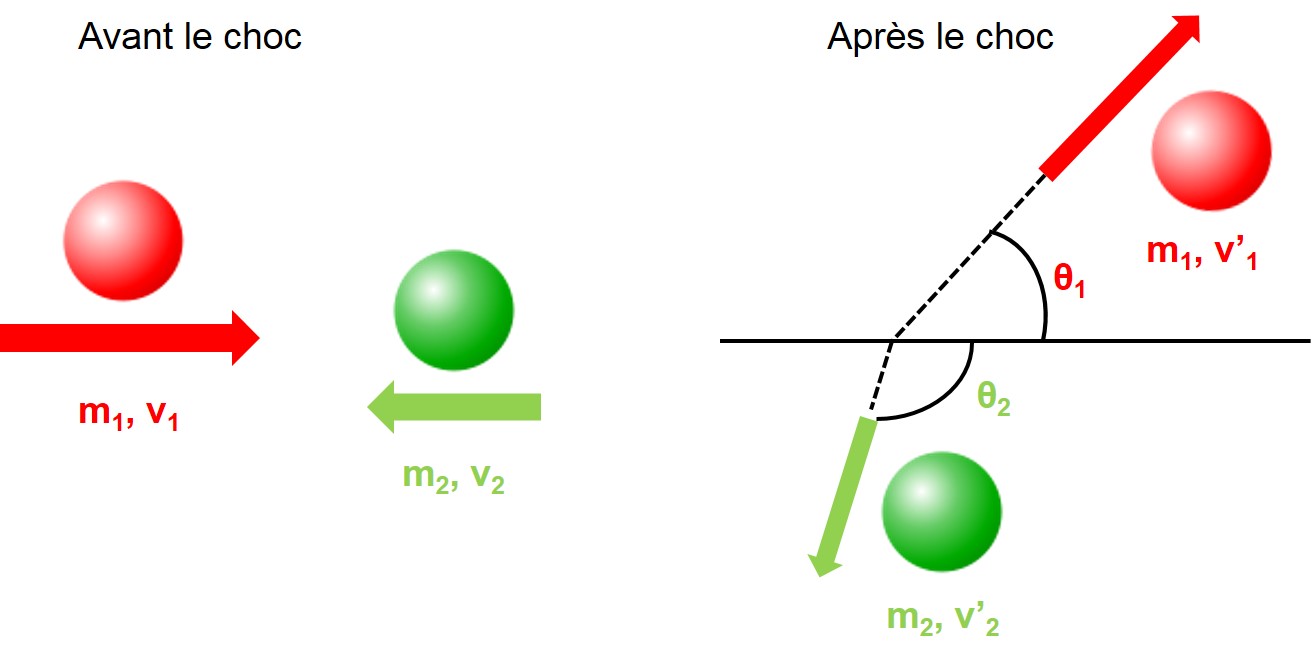
En mécanique classique, si l’on considère par exemple le choc entre deux boules, de masses quelconques (m1 et m2), ce sont les mêmes objets que l’on observe après la collision, émis dans des directions différentes.

Les vitesses et les directions des boules après la collision sont telles que l’énergie et l’impulsion, du système formé par les deux boules, sont conservés lors du choc. En physique classique, l’énergie correspond à l’énergie cinétique et l’impulsion est égale au produit de la masse par la vitesse. Les vitesses et les directions des boules après le choc doivent donc vérifier:

1/2 m₁ v₁² + 1/2 m₂ v₂² = 1/2 m₁ v’₁² + 1/2 m₂ v’₂²

m₁ v₁  – m₂ v₂  = m₁ v’₁  cos(θ₁) + m₂ v₂  cos(θ₂)

m₁ v’₁  sin(θ₁) – m₂ v’₂  sin(θ₂) = 0

Nous avons trois contraintes pour quatre inconnues (v’₁, v’₂, θ₁ et θ₂) ce qui ne nous permet pas de calculer les directions et les vitesses des boules après le choc, à partir de celles de départ. Cette indétermination est réellement présente dans le cas où les boules n’ont ni taille ni structure. Cependant, dans la réalité, avec des boules de taille finie,  une direction sera privilégiée au moment du choc, qui dépend des vitesses, de la nature ainsi que de la distance entre les directions des deux boules incidentes.

Lorsque deux particules élémentaires interagissent, lors d’une collision, la conservation de l’énergie (E)  et de l’impulsion (p) entre les systèmes formés par les deux particules initiales et finales doit être toujours vérifiée. Cependant nous devons faire appel à la relativité restreinte pour définir l’énergie et l’impulsion de chaque particule.

L’énergie n’est plus uniquement celle liée au déplacement mais fait intervenir également la masse de la particule:

E² = p² c² + m² c⁴ où c est la vitesse de le lumière.

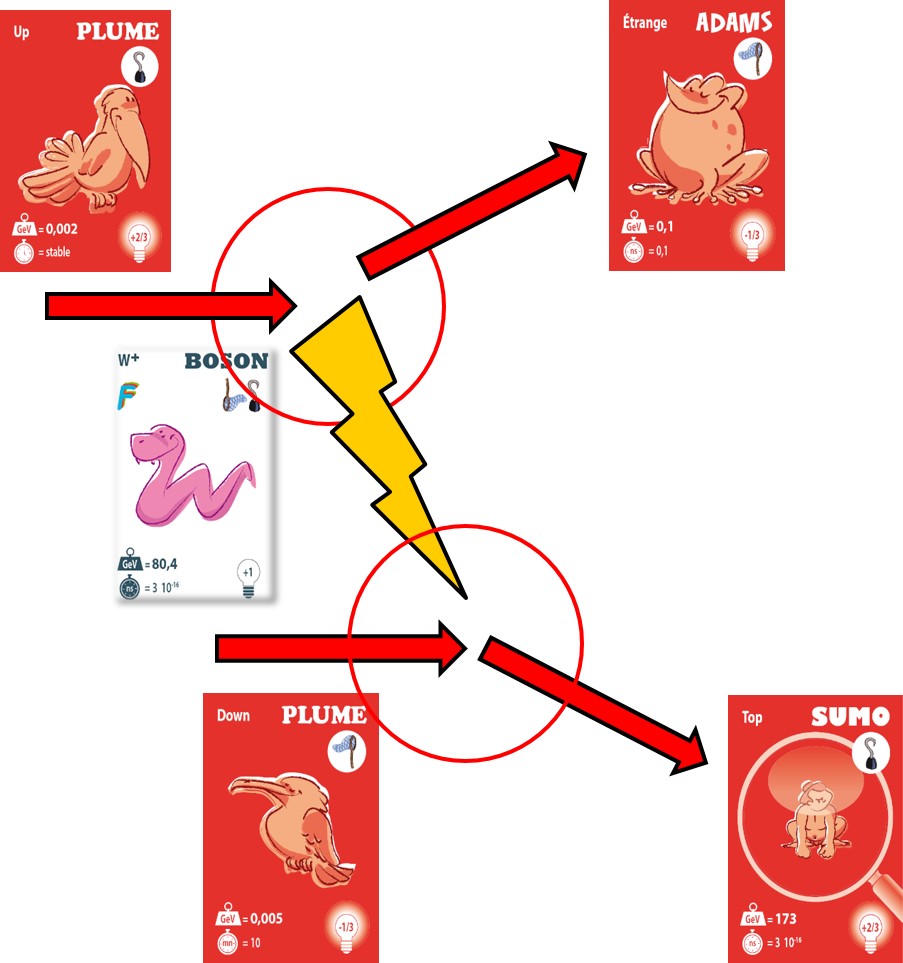
Comme dans l’exemple initial, les propriétés de l’interaction lors de la collision vont privilégier certaines directions dans lesquelles seront émises les particules résultantes. Réciproquement la mesure de ces directions permet aux physiciens d’étudier les interactions fondamentales de la Nature. Contrairement au cas classique il est possible que les particules résultantes ne soient pas identiques aux particules initiales, comme dans l’exemple ci-dessous:

Comme nous l’avons expliqué précédemment, l’interaction entre deux particules élémentaires peut être décomposée en deux étapes, indiquées ci-dessus par les cercles rouges, et dans lesquelles trois particules contribuent. Pour ces interactions, que nous qualifions d’élémentaires, la conservation de l’énergie et de l’impulsion ne peut pas être, le plus souvent, assurée à partir de particules « réelles » (dont la masse est nominale). En effet, la conservation de l’énergie pour la réaction « up » → « étrange » + W⁺ implique que la masse du W ne soit pas égale à sa valeur nominale mais en quelque sorte s’adapte afin d’assurer la conservation de l’énergie et de l’impulsion (les masses des autres constituants ne peuvent être modifiées puisqu’il s’agit de particules observables alors que le W ne l’est pas). On dit que le W est dans ce cas une particule virtuelle.