brelans (32) : les interactions élémentaires

L’interaction entre deux particules élémentaires se produit par l’intermédiaire d’une force qui correspond à l’échange, entre les deux particules de départ, d’une troisième particule (dite particule de force) .

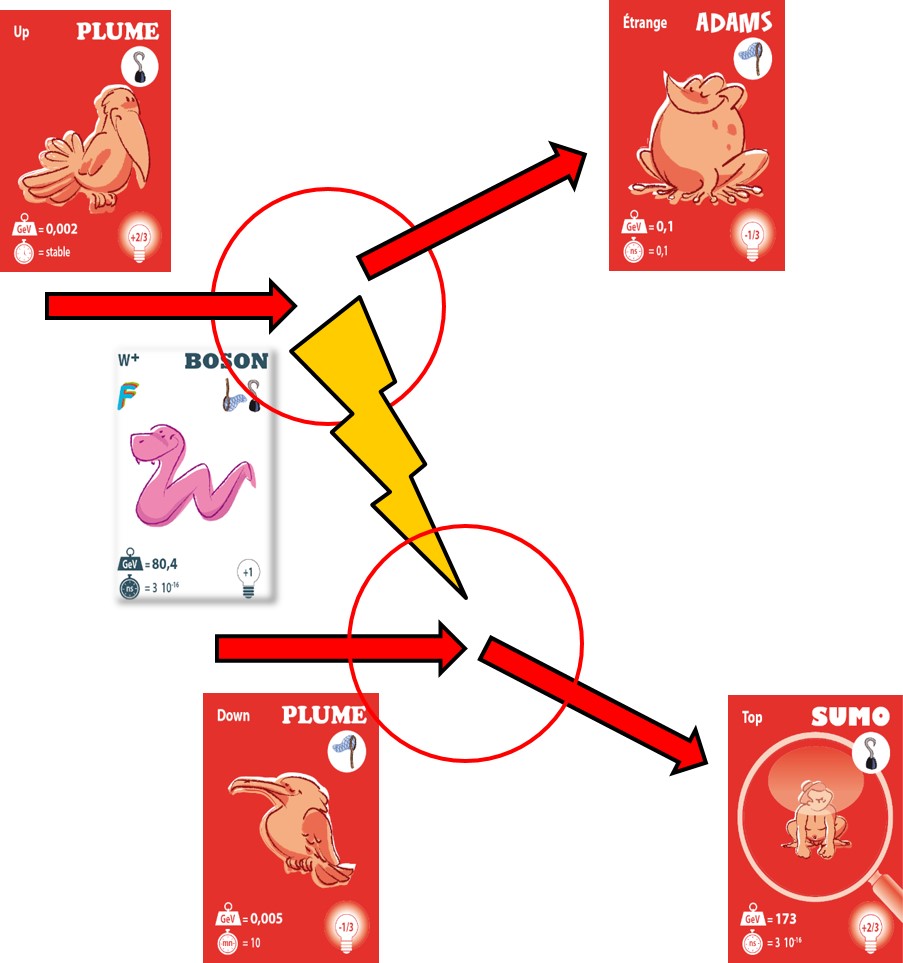
Exemple d’interaction entre deux particules élémentaires dans laquelle un quark « up » rencontre un quark « down » par l’intermédiaire de l’interaction faible représentée ici par le W⁺. Cette interaction conduit à la production des quarks « étrange » et « top ».

Une telle interaction, à laquelle cinq particules élémentaires participent (une « quinte » du Quark Poker), peut être décomposée en deux étapes (« up » → W⁺+ « étrange » puis W⁺ + « down » → « top ») que nous appellerons « interactions élémentaires », et qui sont indiquées ci-dessus par les cercles en rouge. Le choix de l’émission du W⁺ par le quark « up » est arbitraire comme nous le commentons ici.

Les groupes de trois cartes ainsi formés sont les « brelans » du Quark Poker. Ils représentent les différentes possibilités de transformer une particule en deux autres, sous l’action d’une force, en prenant en compte les lois de la physique, illustrées dans ce jeu par la couleur des cartes et par leurs symboles (filet, crochet).

Règles pour former un brelan:

Quatre règles doivent être respectées pour former un brelan. Elles sont résumées ci-dessous et vous pouvez trouver ici des explications simples pour les mettre en œuvre.

Pour l’essentiel, elles traduisent le fait que le code transporté par la particule initiale est la somme des codes des particules résultantes. Ces codes sont représentés sur les cartes par leur couleur et un(des) symbole(s).

une des trois cartes (au moins) doit être une carte blanche (force);
on doit pouvoir former deux groupes, contenant respectivement une et deux cartes, dont les symboles et la couleur sont conservés lorsque l’on passe de l’un à l’autre;
les deux cartes qui ne sont pas une force doivent appartenir à la même famille, à la même antifamille ou bien à une famille et à son antifamille associée. Exception: si la carte blanche est un W et si les deux autres cartes sont colorées, ces dernières peuvent alors appartenir à des familles et des antifamilles différentes. Cette exception est matérialisée sur les cartes des W par une lettre « F » colorée en vert, bleu et rouge
si la force est le photon les deux autres particules doivent être chargées (ampoule allumée).

La première règle traduit le fait qu’une transformation ne peut avoir lieu que sous l’action d’une force.

La seconde règle correspond au fait que le code de la particule qui se transforme est conservé.

Comment mettre en pratique la conservation de la couleur et des symboles entre la carte de départ et les deux autres cartes ? Pour cela, il suffit d’ajouter les couleurs et les symboles des deux cartes et de comparer le résultat à la couleur et au symbole de l’autre carte. Dans ces additions on utilise les conventions suivantes :

la somme d’un symbole et du même, dirigé en sens opposé, donne zéro.
la somme d’une couleur et de son anticouleur correspondante donne zéro. En pratique il n’est pas nécessaire de distinguer entre couleur et anti-couleur, la conservation des symboles implique que l’on a soit la couleur ou l’anticouleur.
les cartes blanches et grises comptent pour zéro au niveau couleur

Visuellement, pour les symboles, la seconde règle peut être vérifiée, sans se préoccuper de l’ordre des trois cartes, en regroupant par deux les symboles identiques présents sur les trois cartes. On doit pouvoir alors former une ou deux de ces paires. S’il reste des cartes, elles doivent représenter le même symbole dans les deux directions opposées. Pour les couleurs, il suffit de s’assurer qu’en plus de la carte blanche, les deux autres cartes ont la même couleur (sans se préoccuper de la distinction entre couleur et anticouleur).

La troisième règle exprime le fait que la plupart des interactions (électromagnétique, la partie de l’interaction faible qui est transmise par le Z⁰ et celle générée par le boson H) ne changent pas le constituant avec lequel elles se couplent (nous verrons que l’interaction forte a également cette propriété). Seule l’interaction faible transmise par les W⁺ et W^– permet de passer d’un quark à un autre, situé ou pas dans la même famille. Cette interaction a pour effet que seules les particules élémentaires les plus légères puissent exister dans la Nature.

Enfin la quatrième règle exprime le fait que l’interaction électromagnétique se manifeste uniquement entre des particules chargées.

Exemples de « brelans au W »:

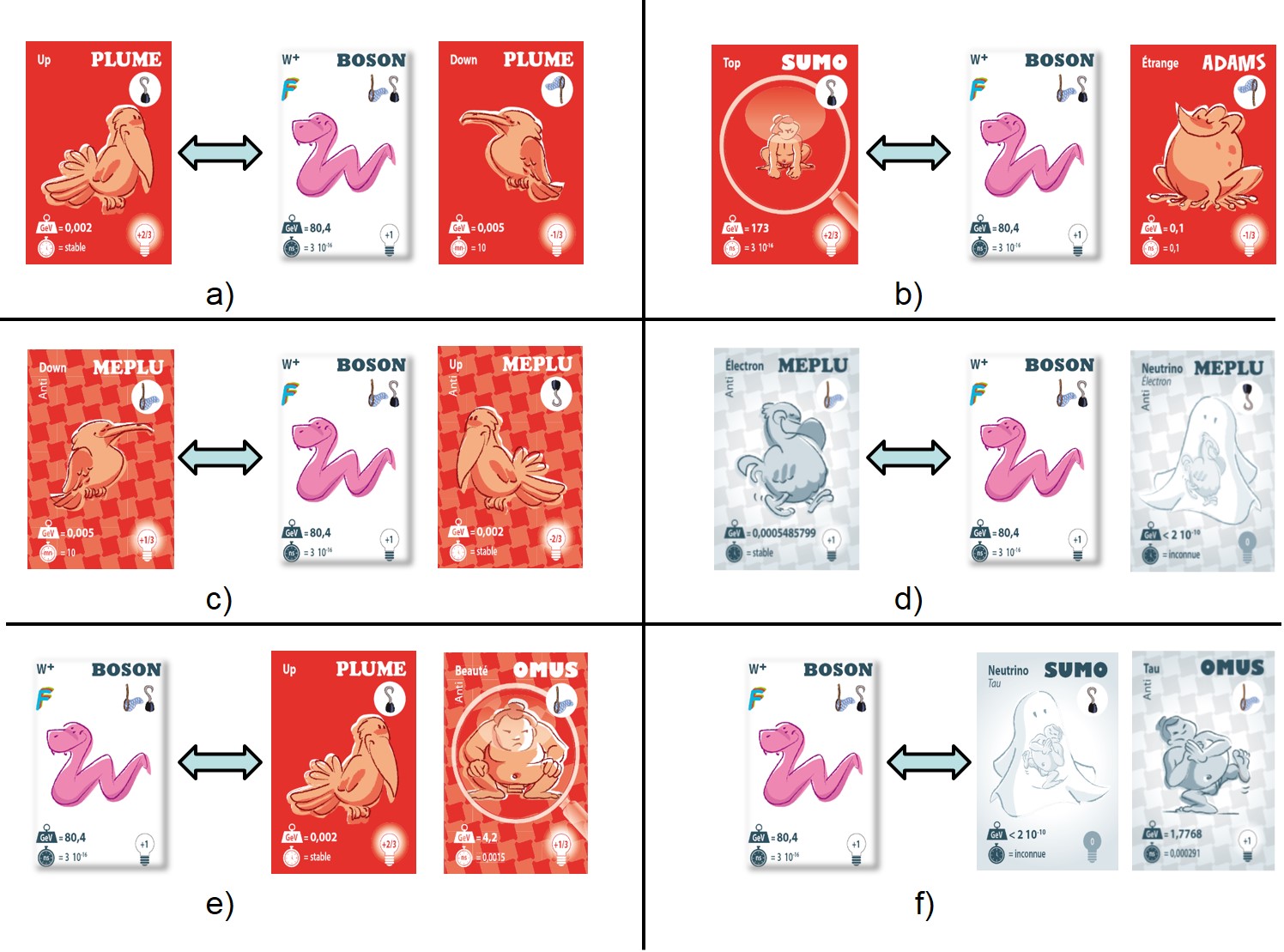
Voici quelques exemples de 3 cartes (brelans) obtenus avec le W⁺ comme force permettant l’interaction.

En plus de la carte blanche, du W, chaque brelan contient deux cartes ayant la même couleur (sans distinguer couleur et anticouleur). On peut vérifier la conservation des symboles entre la première carte et les deux autres. Pour a) et b), la somme des filets, à droite, donne zéro car ils sont dans deux directions opposées. Il reste le crochet vers le haut qui est également présent sur la carte initiale. Pour c) et d) la somme des crochets, à droite, donne également zéro et il reste le filet vers le bas qui est présent sur la carte initiale. Enfin, pour e) et f) on retrouve les deux symboles de la carte de départ (filet vers le bas et crochet vers le haut) sur les cartes finales.

On peut également, sans se préoccuper de l’ordre des cartes, ni de leur interprétation physique, effectuer le comptage des symboles sur les trois cartes; ce qui donne:

+ 2 crochets vers le haut et 2 filets, l’un en bas et l’autre en haut pour a) et b);

+ 2 filets vers le bas et 2 crochets, l’un en bas et l’autre en haut pour c) et d);

+ 2 filets vers le bas et 2 crochets vers le haut pour e) et f);

dans tous les cas on retrouve bien une ou deux (exemples e) et f)) paires de symboles identiques et la somme des symboles restants donne zéro.

Dans les exemples a), c), d) et f) la transformation a lieu entre cartes d’une même famille ou antifamille ou bien entre famille et antifamille correspondantes (« plume » et « méplu » par exemple). Cela est indispensable pour d) et f) par contre on peut utiliser des familles ou des antifamilles différentes si les cartes sont colorées comme pour b) et e).

Brelans « au Z », « au photon » ou « au Higgs »:

Ces trois cartes de force possèdent les mêmes paires de symboles et leur comportement dans le jeu est donc similaire avec toutefois la restriction que les cartes qui peuvent interagir avec un photon doivent être chargées (règle 4) .

Ces trois cartes ont deux paires de symboles et peuvent ainsi interagir soit avec les filets soit avec les crochets (mais pas en prenant un filet et un crochet). Comme les deux symboles dans une paire sont identiques et dirigés dans des directions opposées, l’interaction ne change pas le symbole de la carte initiale (contrairement à l’action des W). D’autre part, comme l’interaction n’a lieu qu’à l’intérieur d’une même famille ou antifamille (règle 3), la particule initiale est inchangée.

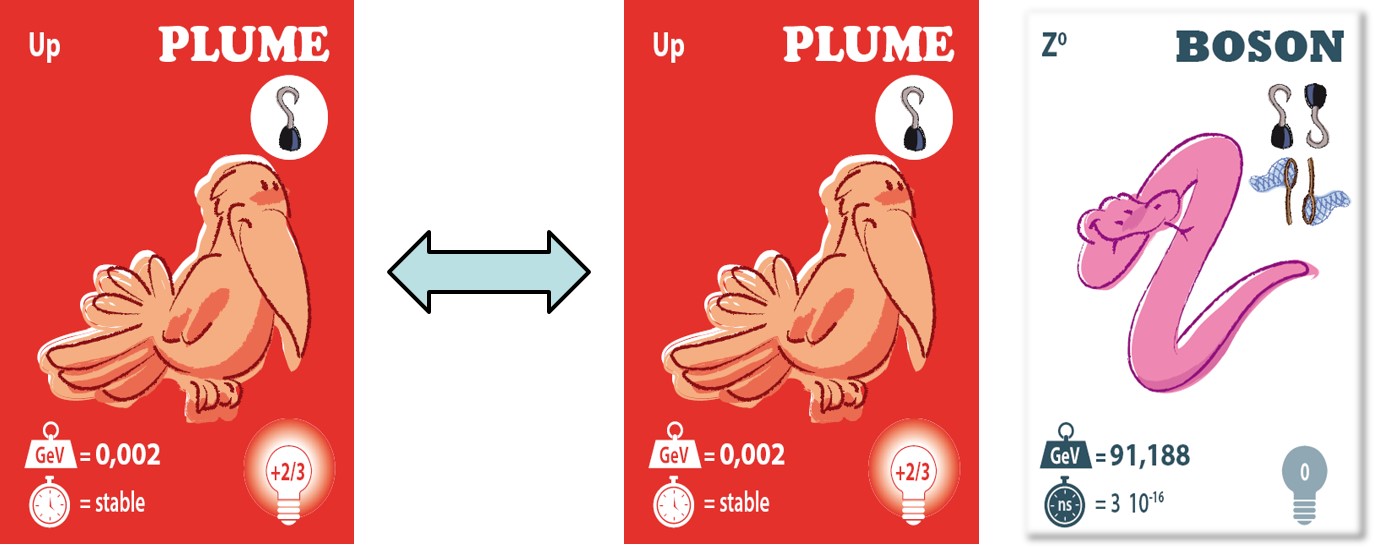
Cependant, le nombre de cartes du paquet va apporter certaines restrictions. En effet, sachant que, dans le jeu, il n’existe pas deux cartes identiques pour représenter les constituants, l’interaction suivante:

est, par exemple, impossible à réaliser dans la pratique bien qu’elle soit parfaitement autorisée entre ces particules.

Dans le jeu, les brelans induits par un Z⁰, un photon ou bien le boson de Higgs sont ainsi restreints aux équivalents des « brelans au W » des exemples e) et f) dans lesquels la particule de force se transforme en une particule et une antiparticule.

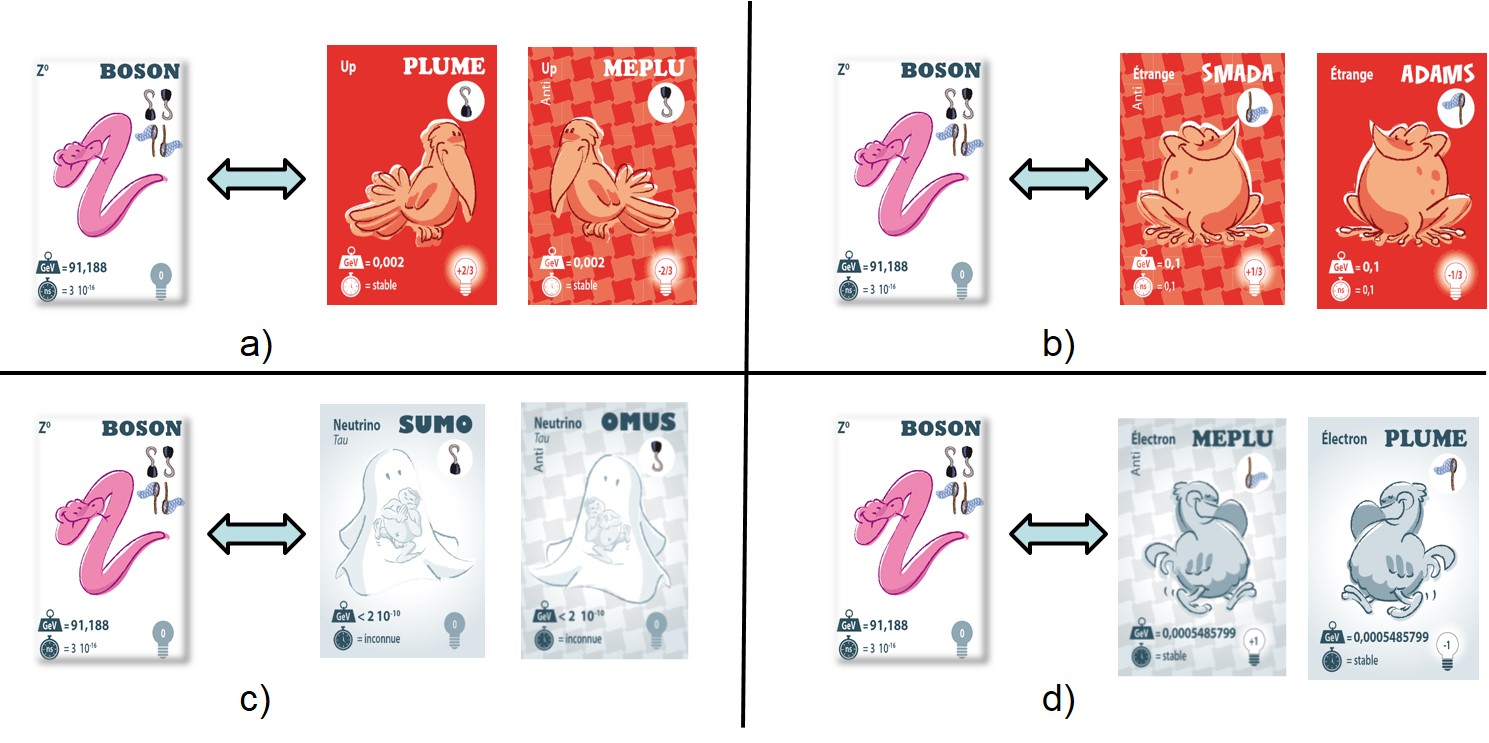
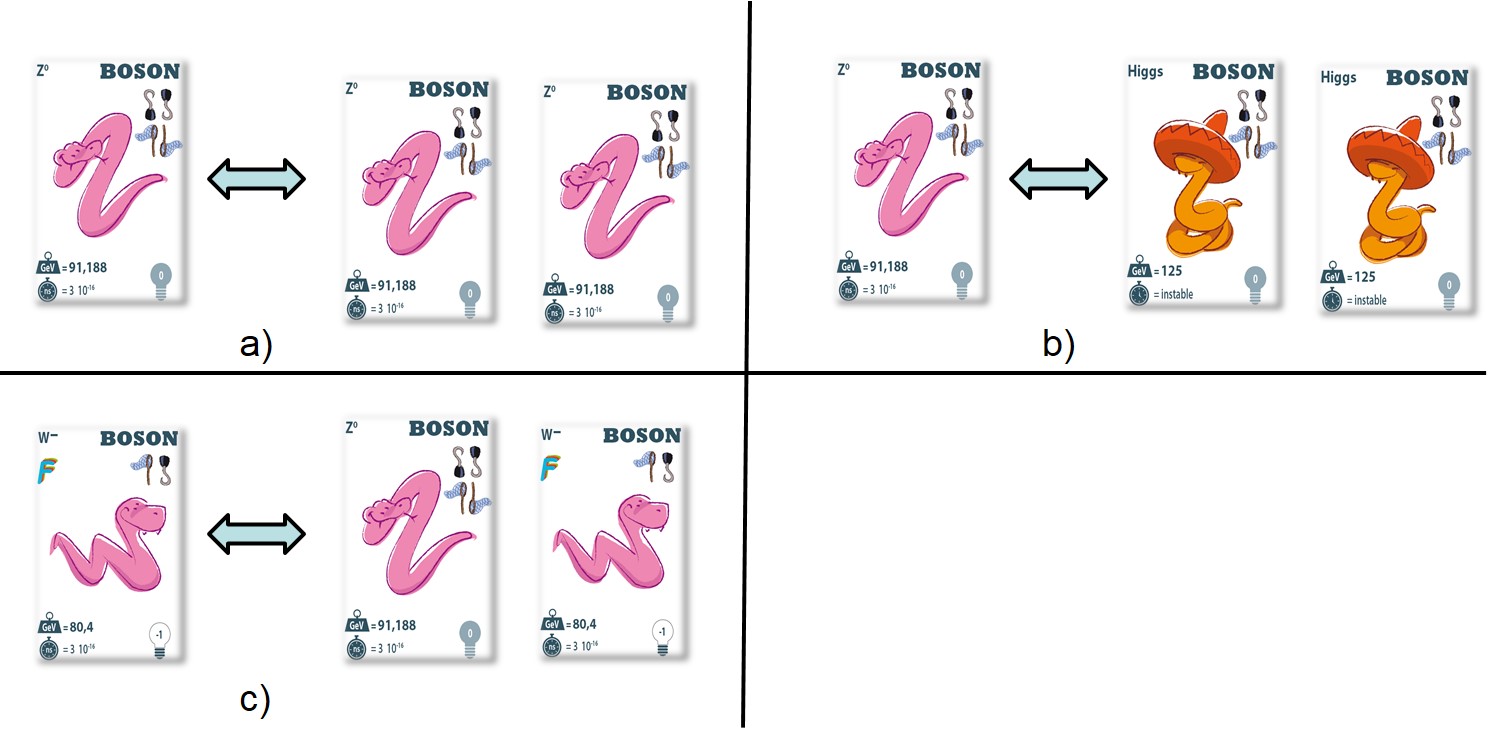
Exemples de « brelans au Z⁰« , on obtient des combinaisons similaires en remplaçant le Z⁰ par un photon ou un boson de Higgs. Pour les photons, l’exemple c) est impossible car les neutrinos sont des particules neutres. Dans les exemples a) et c), le Z⁰ interagit par ses crochets alors que dans les exemples b) et d) il utilise les filets.

Exemples de brelans avec trois forces:

Les forces peuvent également interagir entre elles, les bonnes combinaisons s’obtiennent en appliquant les règles précédentes.

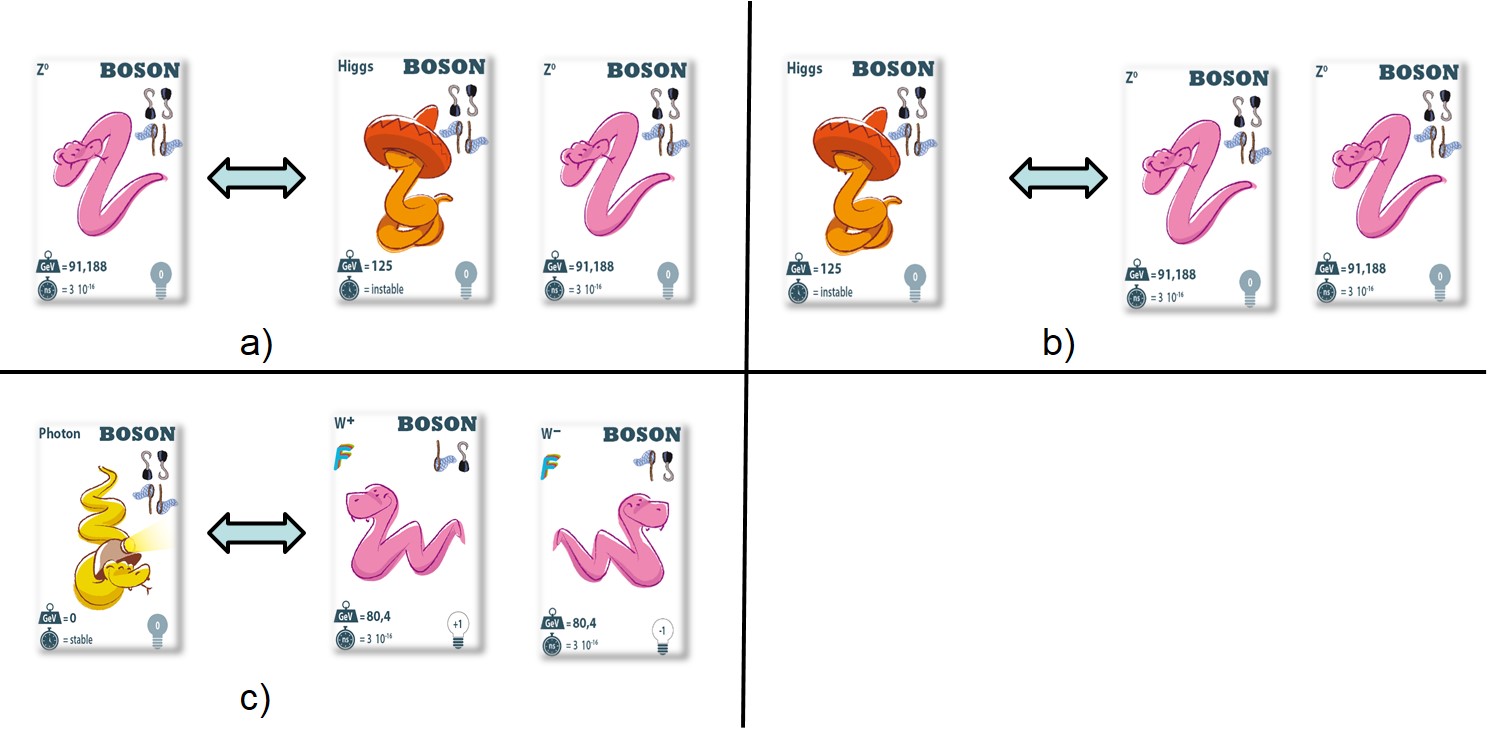
Bien qu’autorisées dans la Nature, certaines combinaisons ne peuvent pas être réalisées à cause des limitations apportées par le paquet de cartes comme, par exemple:

La combinaison de l’exemple a) ne peut pas être réalisée car nous n’avons que 2 cartes Z⁰ dans le jeu. Pour la combinaison b) nous ne disposons que d’une carte « boson de Higgs ». Pour la combinaison c) nous n’avons qu’une carte W^–.

Vous trouverez ci-dessous des exemples de brelans obtenus avec trois forces.

Brelans possibles avec trois forces. Dans l’exemple c), le photon initial peut-être remplacé par un Z⁰ ou bien un boson de Higgs.

Dispositions possibles pour les cartes d’un brelan:

Comme nous l’avons expliqué, il est possible de s’assurer qu’un brelan est correct sans se préoccuper de l’ordre des cartes.

Cependant, afin de distinguer entre une particule qui se désintègre en deux autres, de la fusion de deux particules en une troisième, nous proposons de disposer à gauche les particules initiales:

Représentation de la désintégration 1 → 2 + 3 qui conduit à la transformation du quark « up » (carte 1) en un quark « étrange » (carte 3) par émission d’un W⁺ (carte 2). L’ordre, verticalement, des cartes 2) et 3) est arbitraire.

Les trois mêmes cartes peuvent décrire deux réactions qui se déduisent l’une de l’autre en intervertissant les états initial et final (en effet, les règles de conservation sont des égalités). A la réaction indiquée ci-dessus:

« up » → W⁺ + « étrange »

on peut donc associer la fusion de deux cartes pour en former une troisième: W⁺ + « étrange » → « up ».

Afin de distinguer cette seconde possibilité nous plaçons les deux cartes de départ à gauche:

Fusion du quark « étrange » et du W⁺ pour former un quark « up ». Ces deux présentations correspondent à la meme réaction: 1 + 2 → 3.

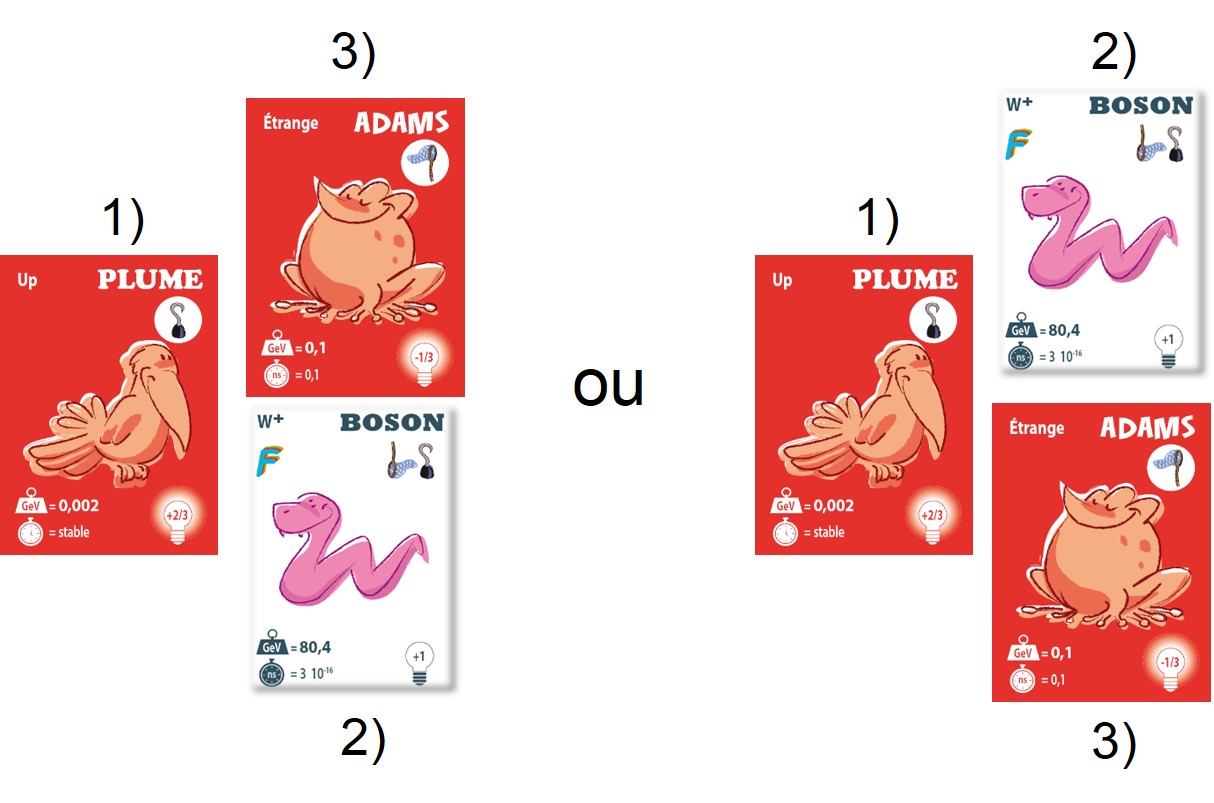
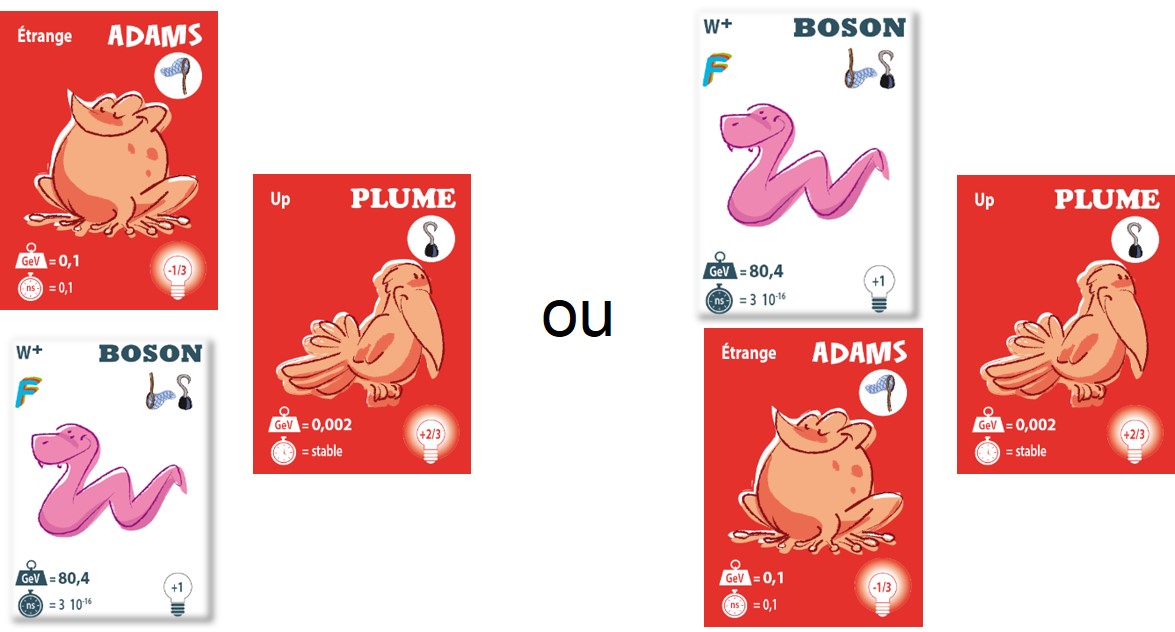
Avec ces conventions, on peut remarquer que d’autres dispositions, obtenues avec les mêmes trois cartes, sont alors incorrectes comme celles indiquées ci-dessous:

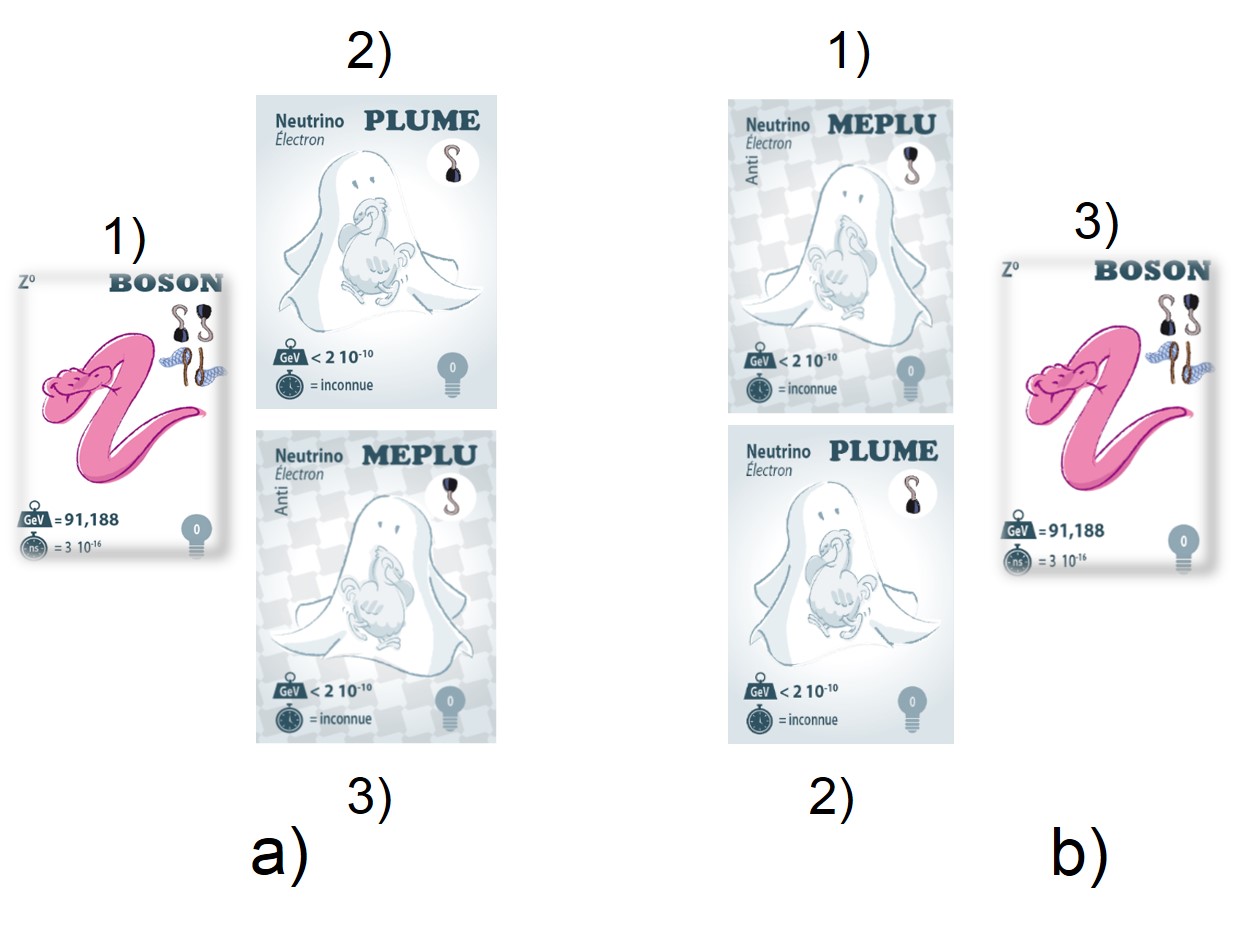
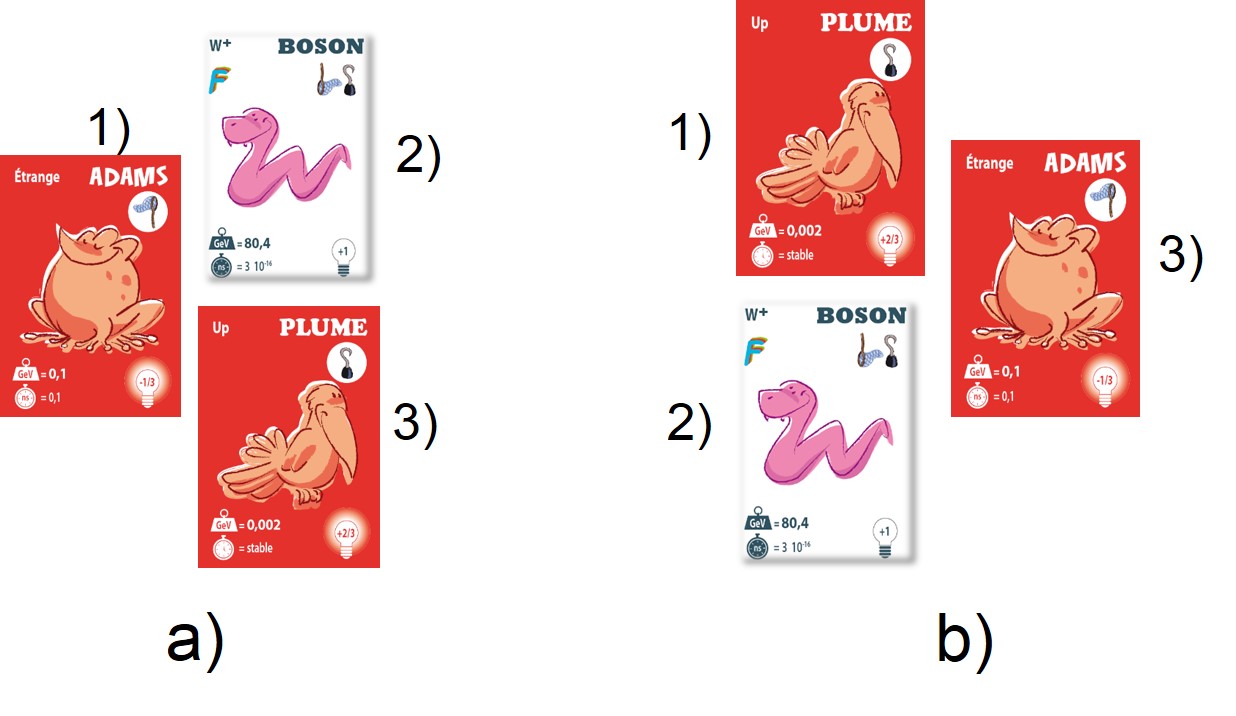L’exemple a) ne peut pas représenter la transformation « étrange » → W⁺ + « up » car le symbole de la carte initiale (filet vers le haut) n’est pas la somme des symboles des deux autres cartes (filet vers le bas et deux crochets vers le haut). De même, dans l’exemple b), et pour les mêmes raisons, le quark « étrange » ne peut résulter de la fusion entre le quark « up » et le W⁺.

Les exemples précédents illustrent le fait que sous l’action d’une force, une particule peut se transformer en une autre particule, éventuellement de nature différente. Les règles précédentes impliquent qu’une particule ne puisse jamais donner naissance à une antiparticule sous l’action d’une force. Par contre, la force elle-même peut se transformer en une paire particule-antiparticule et, inversement, une particule et une antiparticule peuvent fusionner en une force.

Transformation d’un Z⁰en un neutrino-électron et un antineutrino-électron (a). En b), le neutrino-électron et l’antineutrino-électron fusionnent pour former un Z⁰.

Remarque: les conventions proposées pour disposer les cartes d’un brelan seront importantes pour constituer des quintes car ces dernières sont formées par deux brelans qui doivent correspondre à des processus physiques.

Entrainement et dépassement des limites:

Le jeu interactif « Quark Clash », téléchargeable gratuitement sur un PC ou un MAC, permet de s’entrainer à former des brelans. Il permet également de s’abstraire des limitations imposées par la taille et le contenu du paquet de cartes.

Il convient cependant de noter que « Quark Clash » utilise les trois interactions (électromagnétique, faible et forte). Il correspond donc directement au jeu avec 64 cartes.

Conservation de l’énergie et de l’impulsion:

La majorité des transformations élémentaires ne peuvent pas vérifier les lois de conservation de l’énergie et de l’impulsion entre les systèmes existant avant et après la transformation. Nous verrons que les quintes peuvent vérifier de telles contraintes.